When the math nerds refer to a counting system, they use the word base. “We count in base 10,” they proclaim, adding, “Decimal” to sound important. Surely, these are the miracles of mathematics.

Counting systems come into play for programming all the time. To work with digital information, you must grasp binary or “base two.” This system consists of one and zeros and it’s easy to cross your eyes when looking at a binary value:

1011011100001001

So the nerds break up the binary number into clumps of four digits:

1011 0111 0000 1001

Then to save time and space, they translate the value into hexadecimal, the base 16 counting system that has nothing to do with Harry Potter:

0xB709

I’m such a nerd, I was able to translate the binary into hex without looking it up. You can achieve such nerdhood as well! Regardless, ancient neckbeards also know base 8, octal. Here is how you see binary through octal spectacles:

1 011 011 100 001 001

This value translates into:

0133411

The leading zero identifies the value as octal.

For all counting bases, the methodology works the same: Working left to right, each digit place represents the next highest power of the base value. Figure 1 illustrates how this operation works for any base numbering system.

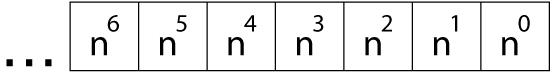
Figure 1. How counting systems represent their values.

For base 10, the digits marching from right to left represent ones, tens, hundreds, thousands, and so on. For base 16 the digits are ones, sixteens, 256s, and so on. You get the picture: If you want to represent any counting base system, each column represents an increased power of the one to its right.

So what if I want to write code that deals with base 3, the ternary (not trinary) counting system? Why, if I really wanted to achieve such a useless level of geekdom, I’d start with the powers of three!

The sample code shown below generates a power table based on the constant base. I avoided using the pow() function and instated relied upon storing each value in the powers[] array, which comes in handy later when I use a powers table to concoct a counting system.

2020_05_30-Lesson.c

#include <stdio.h>

int main()
{
    const int base = 3;
    int powers[11];
    int x;

    /* create the powers table */
    powers[0] = 1;
    for(x=1;x<11;x++)
    {
        powers[x] = powers[x-1]*base;
    }

    for(x=0;x<11;x++)
        printf("%d^%d = %d\n",base,x,powers[x]);

    return(0);
}

Each element number in the array represents a power. Element zero is set to one at Line 10. This preset explains why the loop goes from 1 to 11 instead of starting at zero. It also benefits Line 13, which uses the preceding element (powers[x-1]) to calculate the current element as a power.

Once the array is built, it’s output by a for loop at Line 16.

Here is a sample run:

3^0 = 1
3^1 = 3
3^2 = 9
3^3 = 27
3^4 = 81
3^5 = 243
3^6 = 729
3^7 = 2187
3^8 = 6561
3^9 = 19683
3^10 = 59049

As a constant, you can modify variable base to any other value to generate another powers table. Here’s the output when I change base to 5:

5^0 = 1
5^1 = 5
5^2 = 25
5^3 = 125
5^4 = 625
5^5 = 3125
5^6 = 15625
5^7 = 78125
5^8 = 390625
5^9 = 1953125
5^10 = 9765625

If you want to use larger values for base, change Line 7 so that variable x is a long.

My nefarious purpose here is create a powers of three table. Such a table comes in handy when writing functions that input and output values in ternary. This process starts in next week’s Lesson.

Yes, I’m that crazy.