In last week’s Lesson, I lamented that C lacks a function to compare two floating point values based on a significant number of digits. Being a C programmer, I resolved this issue by writing a function that accomplishes this suddenly necessary task.
Because computers use binary data to store real numbers, precision is an issue: The values 4.0 and 3.99999 might be considered equal by the computer, but values 4.00001 and 4.00001 might not. The issue is precision, which is related to the binary representation of a real number.
To resolve this issue, I need a function that takes two double values and returns the number of matching digits. An example is illustrated in Figure 1.
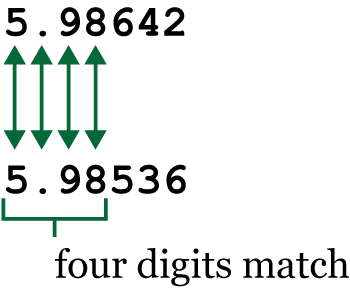
Figure 1. Between the two values, four digits match.
Given the two values above, the function returns 4, the number of matching digits including the decimal. This is the function I wanted when comparing the results of my alternative square root function from last week’s Lesson. Here is the code:
2020_08_01-Lesson.c
#include <stdio.h> /* return the number of matching digits */ int significance(double a, double b) { const int size = 17; char val1[size],val2[size]; int count; /* convert values to strings */ snprintf(val1,size,"%lf",a); snprintf(val2,size,"%lf",b); /* count the matching characters */ count = 0; while( val1[count]!='\0' || val2[count]!='\0' ) { if( val1[count] != val2[count] ) /* bail on mismatch */ break; count++; } return(count); } int main() { int r; double v1,v2; v1 = 5.98642; v2 = 5.98536; r = significance(v1,v2); printf("The values %lf and %lf show %d digits match\n", v1, v2, r ); return(0); }
The wizard behind the curtain in the significance() function is snprintf(), appearing at Lines 11 and 12. This function converts the double values passed into strings, which are more easily compared. The snprintf() function is better than plain ol’ sprintf() in that the n in the name refers to a character count. This extra check makes the function more secure.
The while loop at Line 16 compares the strings, incrementing variable count for each match. This process repeats until the characters don’t match or either string’s terminating null character is encountered.
The value of variable count is returned, which is shown in the output:
The values 5.986420 and 5.985360 show 4 digits match
Various improvements to the code are possible. For example, the function could examine only the portions of the number to the left or right of the decimal. As always, programmers can explore endless ways to keep writing code — especially without looming deadlines.

Some languages give you an epsilon value for their floating point types which is the smallest value which can be represented. You can use it as a sort of “tolerance” or “leeway” for comparisons.
The internet is awash with “bug reports” about comparisons evaluating to false when they should be true, caused of course by the way floating point numbers are represented by, for example IEEE754.
There are a couple of ways of gettin round the problem. If you are handling currencies you can do your calculations in pence, cents or whatever. (Btw why do Americans call cents pennies?)
You can also use some sort of binary coded decimal which uses 4 bits per digit to, in effect, store the number as a string. It’s hideously inefficient though. I once heard that the .NET implementaton was 20x slower than an actual float.
Good info, thanks! I realize my function is weak, but it worked for my purposes.
Cents are still pennies here. They can be found at any merchant, sitting in a little tray to help people make exact change.