Over the past few weeks, I’ve covered the concept of negative integers and their representation as binary values. What can also be represented in binary, something that’s even less obvious than negative values, are fractions.

Seriously: You cannot set half a bit. That makes no sense. You can, however, pretend that part of a binary value represents fractions. Specifically, the bits in the value can represent negative powers of 2.

Normally, each digit in a binary number (integer) represents a positive power of 2. These powers are combined in a binary number to represent any integer, such as the value 19 illustrated in Figure 1.

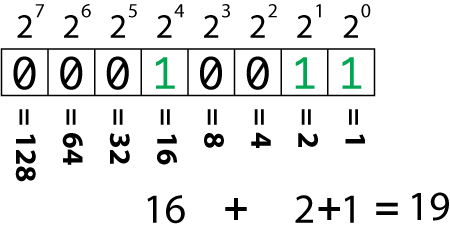
Figure 1. The powers of 2 in a binary value.

Powers of 2 are demonstrated in an earlier Lesson on the pow() function.

It’s my hope that you understand (or at least accept) how the powers of 2 work in a binary value to represent whole numbers or integers.

For fractional values, computer scientists set a bit position as a decimal and to the right of that position interpret the bits as negative powers of 2. The following code demonstrates the negative powers of 2 from zero to -7:

#include <stdio.h>
#include <math.h>

int main()
{
    double t;

    for(t=0.0;t>-8.0;t--)
        printf("2^%.f = %f\n",
                t,
                pow(2.0,t));

    return(0);
}

Here is the output:

2^0 = 1.000000
2^-1 = 0.500000
2^-2 = 0.250000
2^-3 = 0.125000
2^-4 = 0.062500
2^-5 = 0.031250
2^-6 = 0.015625
2^-7 = 0.007812

From the output, you see that each negative power of 2 cuts the previous value in half: 1 becomes ½, ½ becomes ¼, and so on. Figure 2 illustrates how these negative values play out in a byte.

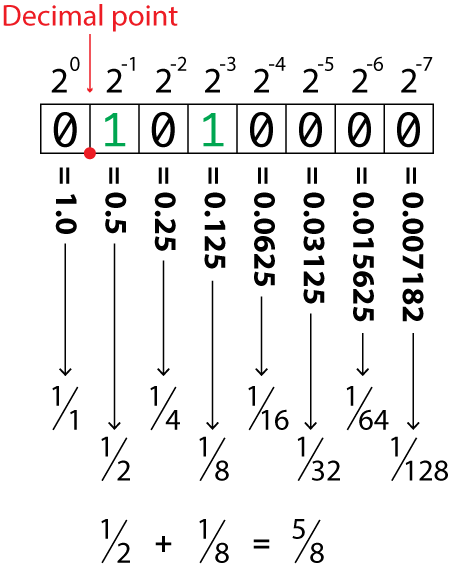
Figure 2. Negative powers of 2 used to represent fractions in a binary number.

Do you see a parallel between the two figures? The holy computer numbers 1, 2, 4, 8, 16, 32, 64, and 128 appear in both binary representations, either as whole number values or as the denominator in a fraction.

In Figure 2, the fraction ⁵/₈ is binary 0101-0000, assuming that the decimal is placed as shown in the figure.

The negative powers of 2 solution hosts a few topics worthy of discussion.

First is the direction in which values are read. As with integers, the bits on the left are greater in value than the bits on the right. This order must be consistent for both positive and negative powers of 2.

Second is the placement of the decimal. In Figure 2, it’s placed between bits 7 and 6. When computer scientists use binary values to show real numbers, the decimal’s location must be consistent. So if the decimal placed in the middle of a 16-bit value, that location must remain consistent or the math doesn’t work.

Finally, playing into the decimal’s location is the concept of precision. Unlike whole numbers, fractions can be all over the map. The decimal value of ⅓ is 0.3333. Using Figure 2, you can only approximate that value as binary 0010-1010 which is 0.25 + 0.0625 + 0.015625, or 0.328125. That’s not exactly 0.3333 but it’s as close as you can come when using only 7 bits of precision.

How do you get a more precise value? You add more bits! Eventually you get close to a true fraction, but no matter how many bits of precision you add, you’ll find a certain degree of slush. This is how float variables are handled in the computer, and why sometimes you find random digits at the end of a floating-point calculation. It all has to do with the binary representation of fractions.