Difficulty: ★ ★ ☆ ☆

The only aspect of math I enjoyed in school was geometry. Trigonometry was a close second. I found the study fascinating and did well; I received a B in that class as opposed by my usual C- or D.

One thing I missed (or slept through) was Heron’s Formula, which is used to calculate the area of a triangle.

The area of a triangle is defined as one-half the base times the height, or ½bh. I drew an illustration in Figure 1 because I’ve had some extra time this morning.

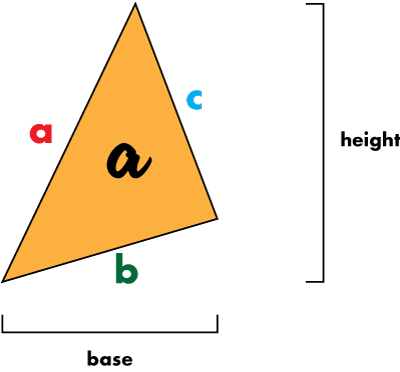
Figure 1. Calculating the area of any triangle: (base*height)/2

Oh, lots of fun can be had with triangles, especially right triangles. But weirdo triangles like the one shown in Figure 1 present an interesting problem when it comes to finding the area. I suppose you could “rotate” the triangle so that one side was flat. But other than using a ruler, obtaining the area isn’t obvious.

What Heron (also known as Hero of Alexandria) did was to concoct a formula whereby you can calculate the area of a triangle when you know the length of each side. To me, this approach seems whacky, but it works. Here is Heron’s formula:

Variables a, b, and c represent the lengths of the three sides of a triangle, as shown in Figure 1. Variable s is the semi-perimeter of the triangle, calculated by using this formula:

As the name states, the semi-perimeter is the total of the three sides lengths divided by two. This value is plugged into Heron’s Formula to obtain the triangle’s area.

I’m certain that lots of interesting mathematical magic is happening to justify how and why Heron’s Formula works. This problem isn’t the one you need to solve. No, your task for this exercise is to write a program that accepts the lengths of three sides of a triangle and generates the triangle’s area as output.

Here is a sample run of my solution:

Input the length of side A: 12
Input the length of side B: 16
Input the length of side C: 20
Semi-perimeter is 24.00
The triangle's area is 96.00 units

Coding the solution is the challenge, but a secondary challenge is to input proper values to represent a true triangle. You just can’t type in any values, as they may not result in a triangular shape. The Wikipedia page on Heron’s Formula features an area calculator. Use it to test values and confirm that the data input creates triangle and to check your answer.

I’ll post my solution in a week.