An on-off bit field is pretty common; you’ll find them all over. Also common are wide bit fields, which can hold values greater than one or zero. These wide bit fields are often mixed with single-bit fields making for a wonderful stew of binary data all held within a single integer value.

As an example, suppose that a chess game uses a bit field to keep track of a specific piece’s location. Two bit fields are required, one for the row and another for the column. The bit fields are organized as shown in Figure 1.

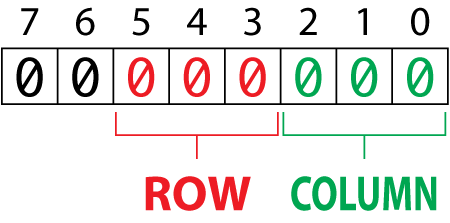
Figure 1. A byte containing two 3-bit fields.

In the figure, you see that three bits are used for both row and column values. Three bits express values from 0 through 7, which is enough to account for 8 rows: 000 through 111. So if the Queen is at row 3, column 8, the binary equivalents would be:

Row 010
Column 111

And the resulting byte would be:

00010111

The nifty part is that you don’t have to strain your head to assembly this binary information; the computer does the job for you. You just need to extract specific bits from the byte to obtain or set the Queen’s position. To code the solution, you need two of the bitwise operators used in previous lessons to extra values: bitwise & (and) and the right-shift operator, >>.

To obtain the row value, the rest of the byte is masked and then the values are shifted right three bits, as illustrated in Figure 2.

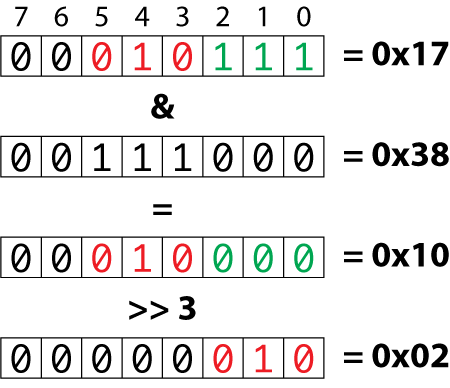
Figure 2. Masking out the row value, then shifting that value right.

The equation & 0x38 masks out the three relevant bits. Next, those three bits are shifted to the right three places. The result is 0x02 (refer to Figure 2), which means that the Queen is at row 3 on the chessboard. (The first row is row zero.)

To obtain the column, bits are masked as well, but the result need not be shifted, as shown in Figure 3.

Figure 3. Masking the column value.

After peeling off the rest of the byte with & 0x07, the remaining value is the column. It just happens to be 7, which is coincidentally the same value as the & (and) mask. And the 7 implies column 8 because, again, numbering starts at column zero.

Here is code that extracts a chess piece’s location from an unsigned char value. The variable is unsigned so that negative results aren’t generated.

#include <stdio.h>

int main()
{
    unsigned char board,row,column;

    board = 23;

    row = board & 0x38;
    row = row >> 3;
    column = board & 0x07;

    printf("The Queen is at row %d, column %d\n",
            row+1,column+1);

    return(0);
}

Here is a sample run:

The Queen is at row 3, column 8

Because a char variable is (usually) 8-bits wide, I could have made the row and column bit fields 4-bits wide each. That would make manipulation easier, plus it would also make the code more readable to anyone who knows hexadecimal and its relationship to binary.

For example, row 2 column 7 would be 0x27 hexadecimal. Also, the bitwise & (and) masks would be 0xF0 and 0x0F. Simple. But not every bit field is exactly 4-bits wide, so rarely will you be so lucky.

In next week’s Lesson, I cover a function that grabs a bit field of any length from any position within a byte.