Oh, how I distrusted recursion when I was a budding programmer. It’s just a tough concept to wrap your head around, especially if you’re an old warhorse Assembly programmer like me who lives in fear of blowing up the stack. Trivial asides aside, recursion often presents an elegant and efficient way to solve a programming puzzle.

This time around, the puzzle is to calculate the golden ratio, φ, which was covered in last week’s Lesson. Figure 1 shows the nifty animation I created to illustrate the ratio, which is wordy and strange to explain, so enjoy the pretty colors.

Figure 1. An animation showing the relationship between ‘a’ and ‘b’ relative to each other.

Last week’s Lesson covered the straightforward way of calculation the value of φ: (1+√5)/2 = 1.6180339887…

Other methods exist to calculate the golden ratio, specifically continued fractions. One such fraction is illustrated in Figure 2. Please! Don’t let its appearance alarm you.

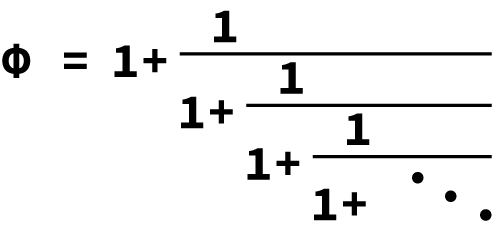
Figure 1. Calculating φ as a continued fraction – something that begs for a recursive function.

These continued fraction boogers can be elegantly transformed into a recursive function. Such an expression may not be obvious at first, but because I’m a nerd and I’ve been doing the programming thing a while, it took only a moment to figure it out:

2020_11_21-Lesson.c

#include <stdio.h>

double phi(double p, int precision)
{
    while(precision)
        return( p + 1/phi(p, precision-1) );
    return(p);
}

int main()
{
    double gr;

    gr = phi(1.0,15);
    printf("The golden radio is %f\n",gr);

    return(0);
}

The phi() function is recursive. Its two arguments are double p, and int precision. The precision argument determines how many times the function recurses, which also plays into the accuracy of the value returned.

Within the return statement, the expression p + 1/phi(p, precision-1) is a representation of the continued fraction shown in Figure 2. This result isn’t calculated until the value of precision reaches zero, and the while loop stops. At this point, the final return statement is executed and the function unwinds, modifying the value of p until the golden ratio is calculated. Here’s a sample run:

The golden radio is 1.618034

I experimented a bit with the precision value passed at Line 15. The value 15 seems to be the minimum required to render a proper value for φ for the digits output.

If I were required to use φ in my code, I would most likely declare it as a defined constant, stretching it out to 20 or so digits as necessary:

#define PHI 1.6180339887498948482

Still, programming is often about exercising the mind as often as it’s about solving math problems. Though recursion can be a frustrating concept, I enjoy working out a recursive function. It can be delightful when it actually works and doesn’t blow up the computer.