To build a number in base 36, you need to know the powers of base 36. This information is required to output digits — 0 through 9 and then A through Z — in the proper order to represent a base 36 value. This task may seem complicated, but it’s the same process that takes place for any counting base.

For example, in base 10, the powers are:

1
10
100
1,000

And so on. For example, and illustrated in Figure 1, the value 4,096 represents 4 thousands, zero hundreds, 9 tens, and 6 ones. Most humans don’t deconstruct numbers in this manner because base 10 (decimal) is what we use.

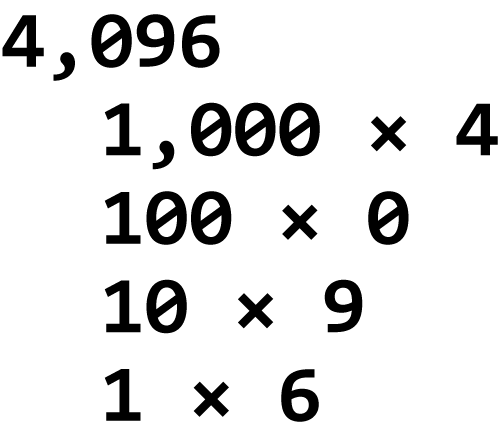
Figure 1. How the decimal value 4,096 works based on powers of 10.

To continue from last week’s Lesson, and represent a number in base 36, I’ve wrote the following code as a start. It builds and outputs the base 36 powers table:

2025_07_05-Lesson-a.c

#include <stdio.h>

#define BASE36_MAX 36
#define SIZE 10

int main()
{
    long b36_powers[SIZE];
    int x;

    /* build the powers table */
    for( x=0; x<SIZE; x++ )
        b36_powers[x] = x ? b36_powers[x-1]*BASE36_MAX : 1;

    /* output the powers table */
    for( x=0; x<SIZE; x++ )
        printf("36^%d = %ld\n",x,b36_powers[x]);

    /* clean-up */
    return 0;
}

The b36_powers[] array holds values representing powers 36⁰ through 36⁹. The following expression is what builds the array:

x ? b36_powers[x-1]*BASE36_MAX : 1

As the value of x increases, the expression b36_powers[x-1]*BASE36_MAX provides the proper power of 36. It takes the previous array value (1 to start) and multiplies it by the BASE35_MAX constant, 36. The loop fills the table, which is then output:

36^0 = 1
36^1 = 36
36^2 = 1296
36^3 = 46656
36^4 = 1679616
36^5 = 60466176
36^6 = 2176782336
36^7 = 78364164096
36^8 = 2821109907456
36^9 = 101559956668416

These are the powers of 36, which are used to translate a decimal value into base 36.

Once the values are known, the following expression sets the proper digits into the correct positions:

( d % b36_powers[x+1])/ b36_powers[x]

Variable d is a decimal value. Its modulus is calculated for a specific value from the b36_powers[] array. The result is divided by the previous powers value, which yields how many units of a certain power translate from decimal to base 36.

Here is the code where this expression works to translate a decimal value into base 36. The output shows how the base 36 powers equivalent of the decimal value:

2025_07_05-Lesson-b.c

#include <stdio.h>

#define BASE36_MAX 36
#define SIZE 10

int main()
{
    long b36_powers[SIZE];
    int b36_values[SIZE];
    int x,d;

    /* prompt for input */
    printf("Enter base 10 value: ");
    scanf("%d",&d);
    if( d<1 )
    {
        puts("Enter a value larger than zero");
        return 1;
    }

    /* build the powers table */
    for( x=0; x<SIZE; x++ )
        b36_powers[x] = x ? b36_powers[x-1]*BASE36_MAX : 1;

    /* translate the decimal value */
    for( x=SIZE-2; x>=0; x-- )
        b36_values[x+1] = ( d % b36_powers[x+1])/ b36_powers[x];

    /* output the values array */
    for( x=1; x<SIZE; x++ )
        printf("36^%d = %d\n",x,b36_values[x]);

    /* clean-up */
    return 0;
}

This code prompts the user for a decimal value. The base 36 powers table is created. The clever expression is used on the decimal value input to pull out the powers of base 36 relative to the decimal value input. The loop runs in reverse order, peeling off larger values first:

for( x=SIZE-2; x>=0; x-- )

The loop stops before x is equal to zero because 36⁰ is one, which won’t help with the translation. (It just adds an extra zero to the result.)

The output shows how the decimal value is translated into base 36 powers:

Enter base 10 value: 12345
36^1 = 33
36^2 = 18
36^3 = 9
36^4 = 0
36^5 = 0
36^6 = 0
36^7 = 0
36^8 = 0
36^9 = 0

For the decimal value 12,345 the result is (skipping leading zeros): 9, 18, 33 in base 36. These values are base 36 digits, placeholders for certain powers. Using my 0-9 A-Z representation, the value of 12,3456 in base 36 is 9IX. This value is described in Figure 2.

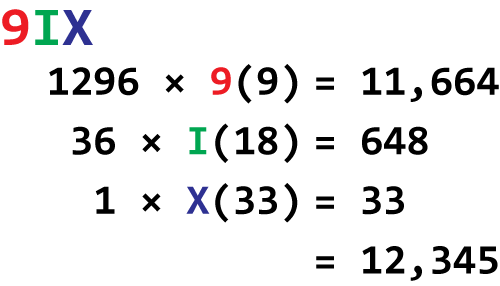
Figure 2. How the base 36 value 9IX translates into decimal.

In next week’s Lesson, I add a function that translates these values into a base 36 string for output.