I enjoy reading about and studying mathematics. One of my favorite books is A History of π. I’ve used this book to inspire my Pi Day (March 14) programs. It’s fascinating stuff.

What I don’t enjoy about mathematics, of course, is doing the math. This conflict is resolved by programming, where I can attempt to pound out a formula and then let the computer toil with the calculations. The compiler is more forgiving than any math instructor, showing me where I’ve erred and giving me a chance to try again.

For this month’s challenge, the topic is Euler’s number, the mathematical constant e. Once again, it’s fascinating to read about this value and even watch YouTube videos (this one is excellent) on how it works and its history.

Figure 1 illustrates the e equation, which was discovered by Italian mathematician Jacob Bernoulli in 1683. The result was calculated by Euler as the value 2.71828182845904523536028747135266250 or thereabouts. It’s one of those magic numbers like π that’s transcendental and irrational — and lots of fun!

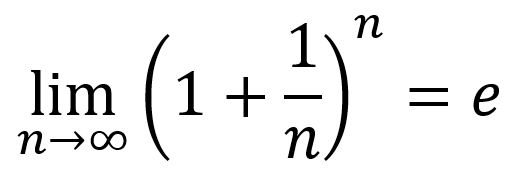
Figure 1. Bernoulli’s equation, which Euler (or Gauss) calculated to the value of e.

In the C language, the e constant is defined in the math.h header file, thus:

#define M_E 2.71828182845904523536028747135266250

Yes, it’s that important.

Your challenge is to write code that calculates the value e. It’s not really that difficult, once you unwind the formula shown in Figure 1 and translate it into C code. But that’s not all! No, you must run and run your the code through a loop in order to obtain the most accurate representation of the value e.

How do you know your calculation is a “most accurate representation”? As your code calculates the value of e, compare your result with the defined constant M_E. The program shouldn’t finish its calculations until both your value and the M_E constant match.

But wait! There’s more . . .

As your code loops, count the iterations. Once the program arrives at the same value as defined constant M_E, output the number of loops it took to make the match. Here’s output from my solution:

The computer calculated 2.718282 after 220825296 loops

TIP: Some platforms require that you link in the math library if you use any C language math functions. The command line switch to do so is -lm (little L, little M).

If you’re using a terminal window to run your solution, use the time command to see how long it takes the computer to arrive at the solution. Here is the output on my iMac Pro running a 3.2GHz 8-Core Intel Xeon W:

The computer calculated 2.718282 after 220825296 loops

real	0m6.678s
user	0m6.672s
sys	0m0.004s

Here is the output on a PC (Intel NUC) running a 3.1GHz Core i7:

The computer calculated 2.718282 after 220825296 loops

real	0m9.696s
user	0m9.688s
sys	0m0.016s

There! I made my PC feel like crap all day! Perhaps you can do the same!

Please try this Exercise on your own before you view my solution.