The challenge for this month’s Exercise is not only to calculate Euler’s number, e, but to count how many loops a program must endure before your e value calculation matches the defined constant M_E. I hope you didn’t find this challenge too difficult.

Yes, I wanted you to write code that loops to calculate the value. Bernoulli’s equation is illustrated in Figure 1. It contains the expression lim n→∞. This mathematical dingus translates into a loop in the C language, not to infinity but to some bignum.

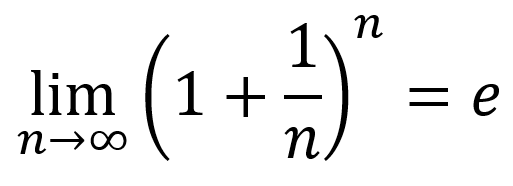
Figure 1. Bernoulli’s equation, which Euler (or Gauss) calculated to the value of e.

Here is how I write Bernoulli’s equation in C:

count = 0;
while(1)
{
    count++;
    e = pow( (1.0/(double)count + 1), (double)count );
}

Variable count is a long integer. It’s initialized to zero and incremented through the loop.

The pow() function raises 1.0/(double)count+1 to the (double)count power, which is the essence of Bernoulli’s equation. Of course, he put it as 1 + 1.0/(double)count, but I reversed it for clarity and precedence and fancy stuff like that.

The double typecasts are required in the expression because using a floating point value as a looping counter is bad practice.

The loop as presented above has no exit condition. To make one, I use the second part of the Exercise’s challenge, which is to match the value you calculate, stored in variable e, with the M_E defined constant. Here is the full code for my solution:

2020_06-Exercise.c

/* link with -lm on Linux */
#include <stdio.h>
#include <math.h>

int main()
{
    long count;
    double e;

    count = 0;
    while(1)
    {
        count++;
        e = pow( (1.0/(double)count + 1), (double)count );
        if( e==M_E )
            break;
    }
    printf("The computer calculated %f after %ld loops\n",
            e,
            count
          );

    return(0);
}

Variable e holds the calculated value of Euler’s number, conveniently also called e. The pow() function within the while loop repeats, refining the value over and over as it approaches, or “tends to,” the value stored in M_E.

Of course, the program can be written without a loop. I mean, the expression does say lim n→∞. So if you just plug in ∞ as a value, it works. Right? (Don’t blanch if you’re a mathematician.) The highest value for an unsigned long int is 4,294,967,295. Why not use it? This code does:

2020_06-Exercise-alt.c

/* link with -lm on Linux */
#include <stdio.h>
#include <math.h>

int main()
{
    double e;
    unsigned long count = 4294967295L;

    e = pow( (1.0/(double)count + 1), (double)count );
    printf("The computer calculated %f for %f\n",
            e,
            M_E
          );

    return(0);
}

No loop is used above. Instead, the maximum size of a long int is specified at Line 8, 4294967295L, the L suffix identifying the value as a long literal. No looping. No waiting. No telling, except for the output:

The computer calculated 2.718282 for 2.718282

Presto.

Still, the looping approach is what I wanted in your solution. If you say, “To hell with him and his silly directions” and concocted a solution similar to my alternative shown above, okay. Still, the notion was to plod through the equation, as the lim n→∞ expression implies. Mathematically, it wouldn’t be any fun otherwise.