I recall the math class where negative numbers were introduced. I was appalled. From Star Trek, I easily accepted the concept of antimatter, but the notion of negative values deeply offended me.

As I learned about computers, negative binary numbers blew me away. In a clutch of bits, which is essentially how values on a computer are stored, how can you have something negative? I mean, binary is just one and zero, right? Where is the negative?

The answer is the sign bit.

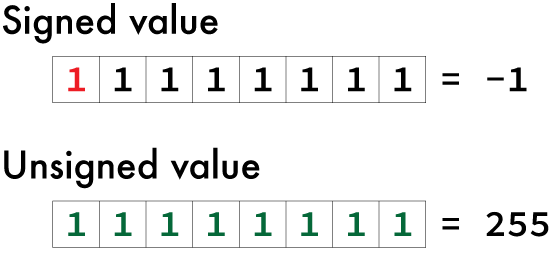
In a binary value, the left-most bit is the sign bit — for signed integer values. The unsigned integer type values treat the bit as part of the number. But for a signed value, the bit is 0 for a positive value or 1 for a negative value, as crudely illustrated in Figure 1.

Figure 1. How the computer interprets signed versus unsigned values.

In Figure 1, the first value shown is -1, binary 11111111 for a signed byte-sized (char) integer value. For the unsigned data type, the value shown is 255. The latter value makes more sense to me. Therefore, to best illustrate how this nonsense works, a program is in order.

2021_04_03-Lesson-a.c

#include <stdio.h>

int main()
{
    signed char a = 0;
    int x;

    for( x=0; x<256; x++ )
    {
        printf("%d\n",a);
        a++;
    }

    return(0);
}

This code loops through char values from 0 to 256. But because variable a is signed, once it huts the value where the sign bit is flipped from 0 to 1, negative values are output. Here is the interesting part of that output:

123
124
125
126
127
-128
-127
-126
-125

After 127 (binary 01111111) the next value is -128 (binary 10000000). Below, I’ve modified the code to include my binbin() function, which is showcased in my C books for outputting binary values:

2021_04_03-Lesson-b.c

#include <stdio.h>

char *binbin(unsigned char n)
{
    static char bin[9];
    int x;

    for(x=0;x<8;x++)
    {
        bin[x] = n & 0x80 ? '1' : '0';
        n <<= 1;
    }
    bin[x] = '\0';
    return(bin);
}

int main()
{
    signed char a = 0;
    int x;

    for( x=0; x<256; x++ )
    {
        printf("%d\t%s\n",a,binbin(a));
        a++;
    }

    return(0);
}

The code runs the same, but with an additional column in the output. Again, here is the interesting part:

123     01111011
124     01111100
125     01111101
126     01111110
127     01111111
-128    10000000
-127    10000001
-126    10000010
-125    10000011

As soon as the 8th bit (for a char) flips, the values output are negative. Further, they flow upward as variable a increments. Eventually, the value returns to zero.

The sign bit is significant for signed integer variables. In fact, you can force-flip the bit so that values turn negative, as demonstrated in the following code:

2021_04_03-Lesson-c.c

#include <stdio.h>

char *binbin(unsigned char n)
{
    static char bin[9];
    int x;

    for(x=0;x<8;x++)
    {
        bin[x] = n & 0x80 ? '1' : '0';
        n <<= 1;
    }
    bin[x] = '\0';
    return(bin);
}

int main()
{
    signed char a = 0;
    int x;

    for( x=0; x<256; x++ )
    {
        a |= 0x80;
        printf("%d\t%s\n",a,binbin(a));
        a++;
    }

    return(0);
}

This code is identical to the preceding example, save for a new Line 24: a |= 0x80. This statement sets the first bit in the byte to 1, which makes all the output negative. Again, the same chunk of output from the sample run as shown earlier:

-5     11111011
-4     11111100
-3     11111101
-2     11111110
-1     11111111
-128    10000000
-127    10000001
-126    10000010
-125    10000011

With the sign bit set, the first part of the output shows negative values, from -128 on up to -1. Then the loop starts over again at -128.

By the way, 10000000 is interpreted as -128 and not “negative zero.” Unlike other programming languages, C lacks an equivalent for negative zero. I explore this notion in next week’s Lesson.