Difficulty: ★ ★ ★ ★
Tetration is a mathematical process that generates obnoxiously huge numbers quickly. It’s exponentiation on overdrive. The concept is insane, but it’s also something you can code in C.
To understand tetration, start with exponentiation. The expression 23 reads as “two to the third power.” It’s shorthand for 2 * 2 * 2. Tetration takes this concept higher, but first consider this operation:
235
The expression above is valid. It’s calculated as 35, which is 243. Then you get 2243, which is 1.4134776518227074636666380005943e+73. Neat-o.
Stacking powers in this manner is called nesting exponents. They work from the top-down. Tetration works similarly, but with a singe value:
222
This expression is evaluated the same: 22 is 4, and 24 is 16: 222 = 16.
One way to express tetration is to use this notation: 22, with the exponent coming before the number. Another way is to use Knuth’s up-arrow notation: 2↑↑2. In computerdom, two carets are often used: 2^^2.
Regardless of the notation, with tetration values can get quite large quickly. Peruse this YouTube video is you want to completely blow your brain. After watching, you may understand why this topic isn’t taught in school or why a tetration function isn’t available in the standard C library. But that doesn’t mean you can’t write one yourself!
This month’s C programming Exercise is to write a tertration function. Pass to the function the base value and the tetration exponent. For the expression 52, the base is 2 and the exponent is 5. This is the same expression depicted in Figure 1. Your function must calculate and return the result.
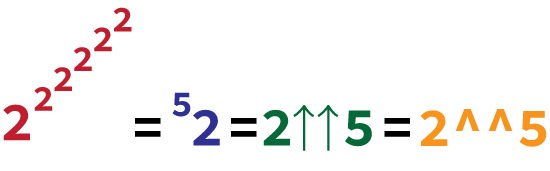
Figure 1. Examples of tetration notation.
You can ignore base values less than 2. I’m unaware whether a rule exists, but I’ve seen nothing regarding a tetration expression like 12, which is just two squared, 22, or 02, which would be one (or would it be two?). Because I’ve not found any documentation to address these low tetration values, just cut off the exponent values below two in your solution.
Here is output from my solution:
Base: 4
Exponent: 3
4^^3 = 13407807929942597099574024998205846127479365820592393377723561443721764030073546976801874298166903427690031858186486050853753882811946569946433649006084096
These numbers get huge quickly! Many of them cannot be calculated when using the standard C library. For example, from Figure 1:
Base: 2
Exponent: 5
2^^5 = inf
Don’t worry about using a large number library to obtain the results, as that’s not part of this exercise.
Please try this challenge on your own. My solution is available here.
Enjoying some free time during the Christmas Holidays, I decided to give this exercise a try—looking through the “Exponentiation Functions” section of the GNU gmp documentation, I first thought of using the mpz_ui_pow_ui() function.
However, while certainly more efficient than the solution I came up with, that felt like too an easy way out… therefore, I decided to implement the “Exponentiation by squaring” (a.k.a. “Binary Exponentiation”) algorithm myself:
#include <gmp.h>
/* GNU Multiple Precision Arithmetic (GMP) /
Multiple Precision Integers and Rationals (MPIR): */
extern void power (mpz_t const base, mpz_t const exp, mpz_t result)
{
/* Set-up: simulate call-by-value (as int are normally passed): */
mpz_t squared_base, shifted_exp;
mpz_init (squared_base); mpz_set (squared_base, base);
mpz_init (shifted_exp); mpz_set (shifted_exp, exp);
/* Function body: */
{ mpz_set_ui (result, 1);
while (mpz_cmp_ui (shifted_exp, 0) > 0)
{
if (mpz_odd_p (shifted_exp))
mpz_mul (result, result, squared_base);
mpz_fdiv_q_2exp (shifted_exp, shifted_exp, 1);
mpz_mul (squared_base, squared_base, squared_base);
}
}
/* Tear-down: free call-by-value helper variables: */
mpz_clear (shifted_exp);
mpz_clear (squared_base);
/*return (result);*/ /* Result already in ‘result’ */
}
extern void tetra (mpz_t const base, mpz_t const height, mpz_t result)
{
/* Set-up: simulate call-by-value (as int are normally passed): */
mpz_t remain_height;
mpz_init (remain_height); mpz_set (remain_height, height);
/* Function body: */
{ mpz_t exp;
mpz_init (exp);
/* mpz_t result = 1; */
mpz_set_ui (result, 1);
/* while (exp > 0) */
while (mpz_cmp_ui (remain_height, 0) > 0)
{
mpz_set (exp, result);
power (base, exp, result);
mpz_sub_ui (remain_height, remain_height, 1);
}
}
/* Tear-down: free call-by-value helper variables: */
mpz_clear (remain_height);
/*return (result);*/ /* Result already in ‘result’ */
}
For this to work, it is necessary to install the “libgmp-dev” package if on Linux; on Windows, the MPIR fork of GMP can be used (with Visual Studio). Iʼve uploaded my solution to GitHub, should anyone be interested: http://tinyurl.com/4mpufjaa