The next update to my pattern-finding program is to hunt down and find a clutch of asterisks in the grid that form a rectangle. Figure 1 illustrates what I’m after.

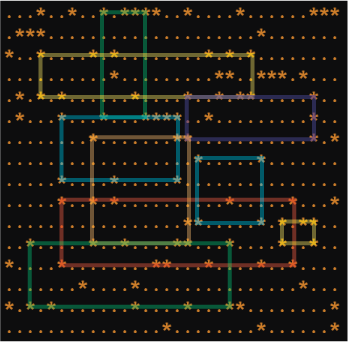
Figure 1. Just a few of the many possible rectangles to be found in the grid.

My approach is has three steps:

1. Scan the entire grid. Use a nested loop to look for any asterisk.
2. When an asterisk is found, look down the same row for an asterisk in that column.
3. Scan across both rows searching for matching asterisks.

These steps mimicked how I found rectangles when I tried this exercise on paper: I scanned down columns first for matching asterisks, then I checked each columns’ rows. You could instead do it by columns and then rows as well. Same difference.

I updated the code from last week’s Lesson, which uses pointers instead of a two-dimensional array.

In the main() function, I constructed the second nested loop, which re-uses variables row and col to plow through the entire grid. A test is added to check for an asterisk:

if( *(grid+row*COLS+col) == '*' )

If true, I call the scan_column() function, which scans down the same column for another asterisk. It’s passed the grid’s address and the current row, column values:

/* look in the current column `c` for a star */
int scan_column(char *g,int r,int c)
{
    int scandown;

    for( scandown=r+1; scandown<ROWS; scandown++ )
    {
        if( *(g+scandown*COLS+c) == '*' )
            return(scandown);
    }
    return(0);
}

The for loop scans down the column, using variable scandown to track the current row. When an asterisk is found, its row value is returned to the main() function. Otherwise, zero is returned.

Upon success (a non-zero value) a second function is called from within the nested loop, find_right(). This function scans both rows for matching asterisks. When found, the column number is returned:

int find_right(char *g,int r1,int c1,int r2)
{
    int f;

    for( f=c1+1; f<COLS; f++ )
    {
        if( *(g+r1*COLS+f)=='*' && *(g+r2*COLS+f)=='*' )
            return f;
    }
    return(0);
}

Upon success, the main() function has the coordinates of four asterisks in the same column/row positions — a rectangle. A count variable is incremented and the coordinate pairs are output.

Here is the full code:

2024_06_01-Lesson.c

#include <stdio.h>
#include <stdlib.h>
#include <time.h>

#define ROWS 16
#define COLS ROWS*2
#define SIZE COLS*ROWS
#define PROB 5

void output_grid(char *g)
{
    int r,c;

    for( r=0; r<ROWS; r++ )
    {
        for( c=0; c<COLS; c++ )
        {
            putchar( *(g+r*COLS+c) );
        }
        putchar('\n');
    }
}

/* look in the current column `c` for a star */
int scan_column(char *g,int r,int c)
{
    int scandown;

    for( scandown=r+1; scandown<ROWS; scandown++ )
    {
        if( *(g+scandown*COLS+c) == '*' )
            return(scandown);
    }
    return(0);
}

int find_right(char *g,int r1,int c1,int r2)
{
    int f;

    for( f=c1+1; f<COLS; f++ )
    {
        if( *(g+r1*COLS+f)=='*' && *(g+r2*COLS+f)=='*' )
            return f;
    }
    return(0);
}

int main()
{
    char *grid;
    int row,col,r,c,count;

    /* seed the randomizer */
    srand( (unsigned)time(NULL) );

    /* allocate grid */
    grid = malloc( sizeof(char) * SIZE );
    if( grid==NULL )
    {
        fprintf(stderr,"Unable to allocate memory\n");
        exit(1);
    }

    /* fill the grid */
    for( row=0; row<ROWS; row++ )
    {
        for( col=0; col<COLS; col++ )
        {
            if( rand() % PROB )
                *(grid+row*COLS+col) = '.';
            else
                *(grid+row*COLS+col) = '*';
        }
    }

    /* output the grid */
    output_grid(grid);

    count = 0;
    /* scan for two in a column */
    for( row=0; row<ROWS-1; row++ )
    {
        for( col=0; col<COLS; col++ )
        {
            /* find a star in the row */
            if( *(grid+row*COLS+col) == '*' )
            {
                /* look for a matching star in the same column */
                r = scan_column(grid,row,col);
                if(r)
                {
                    c = find_right(grid,row,col,r);
                    if(c)
                    {
                        count++;
                        printf("%2d %02d:%02d - %02d:%02d\n",
                                count,row,col,row,c);
                        printf("   %02d:%02d - %02d:%02d\n",
                                r,col,r,c);
                    }
                }
            }
        }
    }

    return 0;
}

Here is a sample run (though not all of it):

......**......*............*....
....*......*.*.*...**...........
...***............*.*.**........
*......*.....*.*.........*...*.*
.........**.........*.*.........
......*.**...*.*....****........
.............**.................
..*..*.*......*.**..........*.*.
.*.....*..........**.*...*.**...
*...*.*....***....**........*.*.
..*..*...*..................*...
..*......*.............*.....*.*
....**..*....*......*..*.......*
........*........*...........*..
...............**.....*....**..*
...*....*...*.........*..*......
 1 01:04 - 01:20
   02:04 - 02:20
 2 01:11 - 01:13
   09:11 - 09:13
 3 01:13 - 01:15
   03:13 - 03:15
. . .
23 09:04 - 09:13
   12:04 - 12:13
24 10:02 - 10:09
   11:02 - 11:09
25 11:23 - 11:31
   12:23 - 12:31

I got so excited with the results that I forgot two things: First, that recursion obviously isn’t need. But more important, the program isn’t really finding all the rectangles; a flaw exists in the code.

In next week’s Lesson, I update the code to graphically output the rectangles. Only then did I discover the flaw.