A harmonic series is a mathematical contraption that deals with cascading fractions. Like the Fibonacci series, I thought I could easily code a harmonic series in C — which I did, but not before reading up on the topic of divergence.

Picking up from last week’s Lesson, a harmonic series is shown in Figure 1, where it represents the total of a series of smaller and smaller fractions. What is the total?

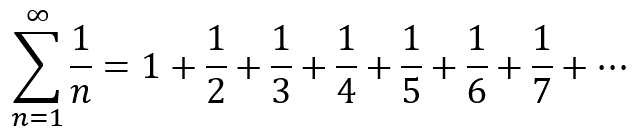
Figure 1. A harmonic series illustrated in a most frightening manner.

Never mind doing the math! What I did was to write computer code that made the calculations for me, adding the values 1/1, 1/2, on up through 1/999. Here is the code:

2020_12_19-Lesson-a.c

#include <stdio.h>

int main()
{
    int x;
    float t;

    t = 1.0;
    for( x=2; x<=1000; x++ )
    {
        t += 1.0 / (float)x;
    }
    printf("The sum of the harmonic series is %.4f\n",t);

    return(0);
}

The for loop at Line 9 does a sum of the first 1,000 items in the harmonic series. Each spin of the loop adds another fraction to the total, from 1/1 to 1/999. After all these spins, here is the output:

The sum of the harmonic series is 7.4855

I felt rather good about myself for performing this calculation, though I then proceeded to increase the looping value from 1,000 to 1,000,000. Here is the new output:

The sum of the harmonic series is 14.3574

Whoa! It’s getting bigger.

Before I increased the looping value further, I wondered what the sum actually was. So I watched the rest of the video on harmonic series only to discover that the series is divergent. Which means that its sum is infinity.

The divergence concept was surprising to me. After studying Zeno’s paradoxes, specifically Achilles and the tortoise, I would think that a harmonic series would flatten out at a certain point. But no! Many proofs abound to show that the series is divergent and continues to grow to infinity.

In fact, in the video, it states that to reach the value of 100.0, my code must loop 15.092×10⁴² times. It would take a computer days to perform this calculation. And somehow it eventually gets to infinity.

Not every series climbs to infinity. In fact, the sum of a series of powers-of-two fractions flattens out to the value 2.0. This series is illustrated in Figure 2.

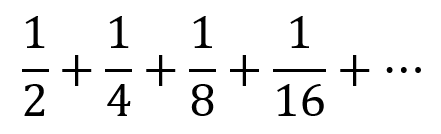
Figure 1. An power-of-two series thing.

My code to generate a power-of-two series hinges upon a for loop:

for( x=2; x<=1000; x*=2 )

This loop generates x values as multiples of 2: 2, 4, 8, 16, and so on. An expression within the loop calculates the sum of fractions 1+1/2+1/4… as illustrated in the Figure.

2020_12_19-Lesson-b.c

#include <stdio.h>

int main()
{
    int x;
    float t;

    t = 1.0;
    for( x=2; x<=1000; x*=2 )
    {
        t += 1.0 / (float)x;
        printf("+1/%d = %.4f\n",x,t);
    }
    printf("The sum of the even series is %.4f\n",t);

    return(0);
}

Line 11 calculates the sum of the powers-of-two series, updating the value in variable t as it goes. Because the values increase rapidly, the code outputs the equations and running total at Line 12. The final total is output at Line 14:

+1/2 = 1.5000
+1/4 = 1.7500
+1/8 = 1.8750
+1/16 = 1.9375
+1/32 = 1.9688
+1/64 = 1.9844
+1/128 = 1.9922
+1/256 = 1.9961
+1/512 = 1.9980
The sum of the even series is 1.9980

Unlike the harmonic series, which grows to infinity, this series approaches 2.0. It is non-divergent, and code easily proves so. None of this would otherwise be interesting to me, but because I can code it in C, it becomes a fun little challenge.